La température est une grandeur importante pour l'Électrotechnicien, elle est à l'origine de vieillissements prématurés des isolants, et de destructions de dispositifs à semi-conducteurs.
Un des objectifs de ce document est de préciser l'origine et les possibilités d'utilisation des grandeurs thermiques rencontrées dans les notices techniques.
Vous y trouverez aussi des applications concernant les échauffements des câbles et des semi conducteurs.
Tous les dispositifs d'électrotechnique ou d'électronique de puissance produisent, comme déchet de leur activité, de la chaleur (effet Joule par exemple).
Plus les possibilités d'évacuation du lieu où elle est produite (âme d'un câble, jonction de semi-conducteur), vers le milieu extérieur (air ambiant...), seront réduites, plus les températures seront élevées, conduisant à des vieillissements prématurés d'isolants, des destructions de jonctions, etc. ...
Il est alors important de connaître la façon dont s'effectuent les échanges thermiques à travers des interfaces plus ou moins bien conductrices de la chaleur (un isolant électrique est aussi, malheureusement, un bon isolant thermique) : c'est l'étude de la conduction thermique.
CONDUCTION THERMIQUE
(fondements théoriques :Théorie générale)
Une puissance P1 s'évacue à travers une "cloison" d'épaisseur Dx, se surface S, et de hauteur suffisante pour qu'on n'ait à se préoccuper que de ce qui ce passe dans le sens des x. A partir du moment où P1 apparaît, celle ci va chauffer la cloison, le reste valant P2 :
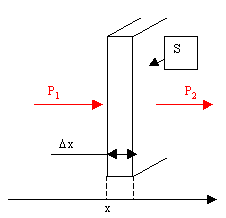
Après un certain temps (cf. Fernand Reynaud), la température en chaque point de la cloison va devenir constante (régime établi), on aura alors P1 = P2
On montre en physique, que l'énergie nécessaire pour élever la température d'un corps est proportionnelle à sa masse m, à l'écart temporel de température Dq, et à une constante c, nommée chaleur massique :
La puissance correspondante :
![]()
On a alors :
![]()
On retrouve bien le fait que, lorsque la température est constante, P1 = P2
En ce qui concerne P2, on montre qu'elle est proportionnelle à la surface d'échange S, à l'écart spatial de température, ainsi qu'à un coefficient l appelé conductivité thermique, caractéristique du matériau de la cloison, et inversement proportionnel à l'épaisseur Dx. Cela se comprend bien dans la mesure où plus P2 est grande, moins la cloison est "isolante" ce qu'on a avec une faible épaisseur, et une grande surface :
![]()
Il faut prendre garde au fait que la température décroît quand on s'éloigne de la source de chaleur, on a donc bien P2 positive. Finalement, on obtient :
![]()
On appelle capacité thermique la quantité :
![]()
et résistance thermique la quantité :
![]()
RÉSISTANCES ET CAPACITÉS THERMIQUES
On peut réécrire l'équation de P1 sous la forme :
![]()
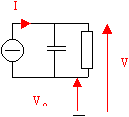
C'est là que l'électricien fait l'analogie avec l'équation et le circuit associé :
|
|
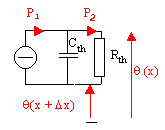
On établit alors un schéma thermique, faisant intervenir capacité et résistance thermique, et dans lequel la puissance joue le rôle du courant. En faisant jouer à la température q(x + Dx) le rôle de "potentiel" de référence :
|
Dans le cas où plusieurs interfaces tentent de s'opposer au passage de P1 :
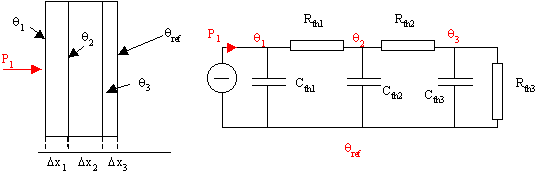
Note sur le choix de la température de référence :
Il est important que cette température soit la plus constante possible, on peut choisir, par exemple celle de l'air ambiant, ou celle d'une barre de refroidissement à eau.
Régime Permanent
Les températures n'évoluent plus dans le temps, c'est à dire que les interfaces ont atteint leur température d'équilibre (les capacités thermiques sont "chargées"), la résistance thermique totale est égale alors à la somme des résistances thermiques :
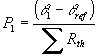
RÉSISTANCE THERMIQUE EFFECTIVE
Lorsqu'on s'intéresse au refroidissement des composants de puissance, ceux ci fonctionnant en commutation, la puissance dissipée dans la jonction est fonction du temps :
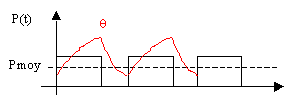
a correspond à la durée de conduction du composant (par exemple 120° pour une diode dans un pont triphasé).
Le schéma thermique correspondant :
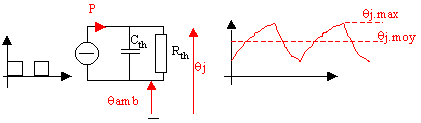
Rth et Cth sont les éléments équivalents à toutes les interfaces (jonction - boîtier, boîtier - radiateur etc...)
qj la température de jonction, qamb la température de l'air ambiant par exemple.
On dispose, après analyse des conditions de fonctionnement du composant, de la puissance moyenne dissipée par la jonction Pmoy.
Aucune puissance moyenne ne peut traverser Cth (analogie avec le courant), la température moyenne de jonction est donc telle que :
![]()
Or, ce qu'il ne faut pas dépasser, c'est la température maximale de jonction, qui, à puissance moyenne donnée, est toujours supérieure à la température moyenne !
Pour déterminer la température maximale, il nous faudrait connaître Cth en plus de Rth. Les fabricants de semi - conducteurs, plutôt que nous fournir ces valeurs et nous abandonner aux calculs, nous donnent une résistance thermique équivalente, fonction de a, appelée résistance thermique effective, et telle que :
![]()
Note : il nous faudrait connaître également les résistances effectives des autres interfaces (radiateur...), il se trouve que les inerties thermiques des autres éléments sont très grandes, et étant donnée la fréquence des phénomènes étudiés ici (50 ou 60Hz), on peut considérer la température du boîtier comme constante (cf. Ordres de grandeur)
Pour plus de renseignements et notamment les variations de la résistance effective en fonction de la durée de conduction : Développement
IMPÉDANCE THERMIQUE TRANSITOIRE
Supposons un composant en fonctionnement normal, dissipant une puissance P et ayant atteint l'équilibre thermique représenté par une température moyenne qmoy.
Lorsqu'une surcharge DP se produit, on a besoin de connaître l'élévation de température Dq qu'elle entraîne, de façon à vérifier que la température maximale n'est pas atteinte.
Pratiquement, on se pose le problème de savoir quelle surcharge (de quelle amplitude et de quelle durée) sera admissible par le composant, avant que les protections n'agissent, les temps de réaction de celles-ci étant de l'ordre de la dizaine de millisecondes.
C'est la notion d'impédance thermique transitoire qui permet de définir cela :
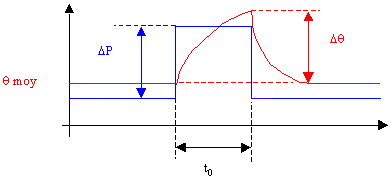
L'impédance thermique transitoire Zth, fonction de t0, est définie par :
![]()
On trouve facilement que :
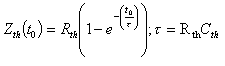
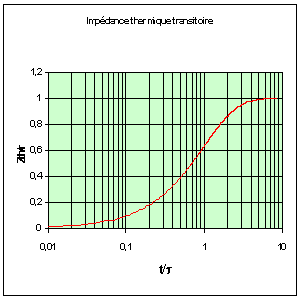
Pour une durée de surcharge suffisamment longue, l'impédance thermique transitoire se confond avec la résistance thermique.
On donne ci - dessous les variations de Zth/Rth en fonction de t0/t. Notez bien que l'axe des abscisses est en coordonnées logarithmiques comme il est d'usage de le faire . Les fabricants donnent la courbe Zth en fonction de t0 pour chaque composant.
Visitez par exemple :http://www.semikron.com
APPLICATION : Protection thermique des composants à semi-conducteurs