
Le transformateur est un convertisseur d'énergie électrique AC / AC isolé. Les deux fonctions principales sont la transmission isolée d'énergie et la modification du niveau d'une source alternative.
1- Description - Exemple de constitution
Aspect extérieur
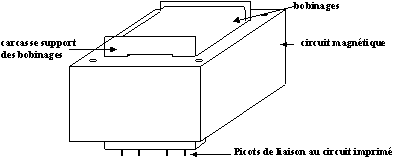
Circuit magnétique seul
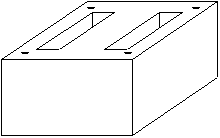
Réalisation du circuit magnétique par empilement de tôles
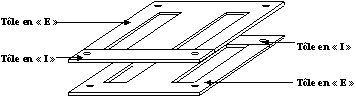
Les tôles ont une épaisseur entre 0,4 et 0,7 mm en fonction du soin qui est exigé par l'application. L'empilement de plan des tôles en " E " et en " I " avec alternance des joints entre le " E " et le " I " permet de fabriquer le circuit magnétique. L'ensemble forme un bloc cohérent quand cet ensemble est collé ou par serrage grâce aux systèmes vis écrous qui prennent place dans les trous. Les plans de tôle sont isolés entre eux par l'oxydation naturelle des tôles ou par un vernis. Ainsi les pertes par courant de Foucault sont limitées.
Position des enroulements sur la carcasse
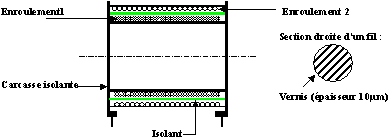
Chaque spire est isolée de sa voisine grâce au vernis isolant déposé sur le fil du bobinage. Une fois le bobinage constitué, la carcasse et ses enroulements sont déshydratés et imprégnés avec un vernis qui polymérise en étuve.
2- Modélisation du transformateur
2.1- Symboles
![]()
2.2- Transformateur idéal
Hypothèses
- pas de pertes dans les conducteurs
- pas de pertes dans le noyau magnétique
- perméabilité infinie du circuit magnétique
- couplage magnétique parfait des enroulements
Équations
Le noyau magnétique de section droite S est homogène.
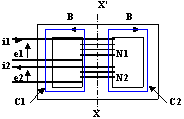
Les deux contours C1 et C2 sont symétriques par rapport à l'axe XX' et enlacent les mêmes courants et s'appuient sur des circuits magnétiques de mêmes dimensions. C'est donc la même induction B qui circule sur ces deux contours.
![]() C H.dl =
C H.dl = ![]() i = N1.i1 - N2.i2
i = N1.i1 - N2.i2
e1 = -N1.S.db/dt
e2 = -N2.S.db/dt
Dans l'hypothèse d'une perméabilité infinie, H = 0 et ![]() C H.dl = 0 = N1.i1 - N2.i2
C H.dl = 0 = N1.i1 - N2.i2
Alors : e2/e1 = N2/N1 = i1/i2 = m où m est le rapport de transformation.
Observations
- b = (-1/[N1.S])
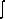 C e1.dt, l'application d'une composante continue de tension sur les enroulement sature le matériau magnétique, dans ce cas le courant appelé tend vers l'infini. Le transformateur ne supporte pas les tensions continues.
C e1.dt, l'application d'une composante continue de tension sur les enroulement sature le matériau magnétique, dans ce cas le courant appelé tend vers l'infini. Le transformateur ne supporte pas les tensions continues. - Si la source d'énergie est connecté à l'enroulement 1, ce dernier porte le nom de primaire, l'enroulement 2 s'appelle alors le secondaire.
- La forme d'onde de e2 est la même que celle de e1.
- La forme d'onde de i1 est la même que celle de i1.
- Les signaux doivent être alternatifs (sinusoïdaux, carrés, triangulaires,...).
- e1.i1 = e1.m.i2 = e2.i2, la puissance instantanée appliquée au primaire est directement transférée au secondaire sans accumulation d'énergie. D'autre par la puissance est conservée bien que les tensions et courants au primaire et au secondaire soient différents.
- Si la source d'énergie est une source de tension, la tension e1 est imposé et indirectement e2 telle que e2 = m.e1. La charge connectée au secondaire appelle un courant i2 (loi d'Ohm). Le courant i1 est alors la conséquence de i2 au rapport m près.
- Si la source d'énergie est une source de courant, le courant i1 est imposé et indirectement i2 tel que i2 = i1/m. La charge connectée au secondaire du fait de ses propriétés détermine la tension e2. La tension e1 est alors la conséquence de e2 au rapport m près.
2.3- Transformateur réel
Bilan des imperfections
- Pertes par effet Joule dans les conducteurs
- Pertes dans le noyau magnétique par courant de Foucault et par hystérésis
- perméabilité finie du circuit magnétique
- couplage magnétique imparfait des enroulements
Modélisation du transformateur réel

Les éléments du modèles sont parfaits et chacun correspond à la prise en compte d'une imperfection autour d'un transformateur parfait de rapport de transformation m :
- R1 = résistance du fil de l'enroulement primaire
- R2 = résistance du fil de l'enroulement secondaire
- m = rapport de transformation
- Rpf est une résistance image des pertes fer (Pf)
En sinusoïdal l'induction maximale (Bm=E1/[4,44.N1.S.f]) est proportionnelle à E1. Et les pertes dans le fer varient proportionnellement à Bm2. Dans le modèle on vérifie que Rpf dissipe E12/Rpf, il existe donc une valeur de Rpf telle que Pf = E12/Rpf.
- Lm est l'inductance de magnétisation.
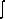 C H.dl =
C H.dl =  i = N1.i1 - N2.i2 =
i = N1.i1 - N2.i2 = 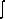 C (b/µ0.µr).dl
C (b/µ0.µr).dl
Avec dans le noyau magnétique réel µr finie, N1.i1 - N2.i2 0
0
Alors N1.i1 - N2.i2 = .Lm.i10 (
.Lm.i10 ( est la réluctance du noyau magnétique).
est la réluctance du noyau magnétique).
-
lf1 et lf2 sont respectivement les inductances de fuite primaire et secondaire.
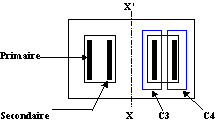
Sur C3, ![]() C3 H.dl = N1.i1
C3 H.dl = N1.i1
Sur C4, ![]() C4 H.dl = N1.i2
C4 H.dl = N1.i2
Puisque la circulation de H sur les contours C3 et C4 est non nulle, C3 et C4 portent des lignes d'induction. Mais ces lignes d'induction ne sont pas enlacées simultanément par les enroulements primaire et secondaire. On les appelle des lignes d'induction de fuite.
La loi de Faraday s'applique en tenant compte du flux commun ![]() c (enlacé par tous les enroulements), du flux de fuite primaire
c (enlacé par tous les enroulements), du flux de fuite primaire ![]() f1 (enlacé par le primaire seul) et du flux de fuite secondaire
f1 (enlacé par le primaire seul) et du flux de fuite secondaire ![]() f2 (enlacé par le secondaire seul) :
f2 (enlacé par le secondaire seul) :
e'1 = -N1.(d![]() c/dt) -N1.(d
c/dt) -N1.(d![]() f1/dt) = e1 + lf1.(di1/dt)
f1/dt) = e1 + lf1.(di1/dt)
e'2 = -N2.(d![]() c/dt) -N2.(d
c/dt) -N2.(d![]() f2/dt) = e2 + lf2.(di2/dt)
f2/dt) = e2 + lf2.(di2/dt)
3- Cas du transformateur de distribution
Les transformateurs utilisés dans la distribution d'énergie électrique (plus de 1kW) doivent fournir une tension au secondaire très stable (à 2 ou 3% près) quand I2 varie. Dans ce cadre l'hypothèse de Kapp est applicable. L'objectif de la modélisation est de prévoir cette variation avec précision.
3.1- Modélisation à partir de l'hypothèse de Kapp
Hypothèse de Kapp
Le flux magnétique dans le circuit magnétique est invariant vis à vis de l'état de charge du transformateur.
L'induction maximale dans le fer est Bm = E1/(4,44.N1.S.f). Faire l'hypothèse que Bm est constante vis à vis de i1 et i2 équivaut à considérer constante la tension sur l'inductance de magnétisation.
Autre conséquence de l'hypothèse de Kapp, les pertes fer sont constantes. Cela revient à placer Lm et Rpf en tête du modèle.
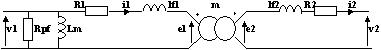
Vu des bornes du secondaire le transformateur est un générateur de tension

La résistance Rs parcourue par i2 doit dissiper l'ensemble des pertes Joule du transformateur,
Rs.I22 = R2.I22 + R1.m2.I22. Donc Rs = R2 + m2.R1
L'impédance Xs parcourue par i2 doit consommer la même puissance réactive que lf1 et lf2,
Xs.I22 = lf2.w.I22 + lf1.m2.I22. Donc Xs = (lf2 + m2.lf1).w
Équation de la maille du modèle vue du secondaire : V2 = m.V1 - Rs.I2 - jXs.I2
Le diagramme de Fresnel associé est appelé diagramme de Kapp :
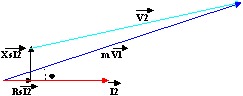
En fait dans un transformateur de distribution Rs.I2 et Xs.I2 sont très petits devant V2 et m.V1. Alors les vecteurs mV1 et V2 ont pratiquement la même direction.
Hypothèse d'Arnold : ces deux vecteurs mV1 et V2 ont même direction.
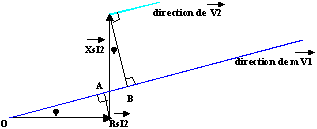
Dans l'hypothèse d'Arnold les vecteurs V2 et mV1 sont colinéaires et la chute de tension au secondaire ![]() U2 se calcule algébriquement.
U2 se calcule algébriquement. ![]() U2 = mV1 - V2
U2 = mV1 - V2
Sur la figure ![]() U2 correspond à OB = OA + AB
U2 correspond à OB = OA + AB
OA = Rs.I2.cos![]()
AB = Xs.I2.sin![]()
DU2 = Rs.I2.cos![]() + Xs.I2.sin
+ Xs.I2.sin![]()
3.2- Détermination expérimentale des paramètres du transformateur
Cette expérimentation s'effectue lorsqu'il faut prévoir le comportement d'un transformateur et que l'essai direct est impossible.
Les essais ne doivent mettre en jeu que des faibles puissances :
Essai à vide
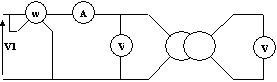
On mesure sous V1 = V1n à f = fn, P10, I10,V20
Rpf = V102/P10
Cos![]() 10 = P10 / (VI0.I10)
10 = P10 / (VI0.I10)
Q10 = P10.tg![]() 10
10
Lm = V102 / Q10
m = V20 / V10
Essai en court circuit sous tension réduite
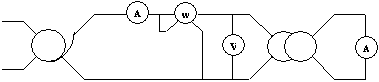
On mesure à I2n = I2cc et f = fn, P1cc, V1cc, I1cc.
Rs = Pcc / I2cc2
cos![]() cc = Pcc / (V1cc.I1cc)
cc = Pcc / (V1cc.I1cc)
Xs = Rs.tg![]() cc
cc
4- Cas du transformateur d'intensité
Le transformateur d'intensité est utilisé dans les mesures de courant pour ses fonctions d'isolation et de mise à l'échelle. Exemple mesure du courant sur un réseau 5kV / 1000A.
4.1- Symbole du transformateur d'intensité
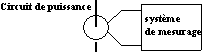
Dans ce contexte la caractérisation du transformateur se fera au point de vue de la sécurité et de la précision dans le rapport des courants primaire et secondaire.

Les courants qui traversent Rpf et Lm doivent être les plus petits possible pour que i1 / i2 s'approche de m. La fabrication du circuit magnétique emploie des matériaux nobles pour augmenter Rpf. Par contre les paramètres R1, R2, lf1 et lf2 ont une influence modeste dans une chaîne de mesure de courant. Le modèle du transformateur en fera donc abstraction.
4.2- Modèle du transformateur d'intensité
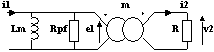
La résistance R est soit la résistance interne d'un appareil de mesure, soit un " shunt " de mesure qui a pour vocation de créer une tension v2 proportionnelle à i1.
Mais v2 impose e1 qui détermine la consommation de Lm et Rpf. Il faut donc que v2 soit la plus faible possible. Pour des raisons de facilité d'exploitation V2 est choisi autour de 100mV.
Le comportement en fréquence du transformateur est de type passe haut.
4.3- Structure pour améliorer le comportement du transformateur d'intensité
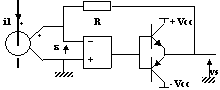
Ici ![]() = 0 et le transformateur d'intensité fonctionne à merveille puisque les courants dans Lm et Rpf sont infimes. Vs = -R i1/m
= 0 et le transformateur d'intensité fonctionne à merveille puisque les courants dans Lm et Rpf sont infimes. Vs = -R i1/m
Les transistors permettent d'éviter un trop fort rapport m qui rendrait la fabrication du transformateur difficile. En effet le transformateur peut délivrer ![]() fois le courant de l'ALI.
fois le courant de l'ALI.
5- Transformateur d'impulsions
Le transformateur d'impulsions est un composant électronique dont la vocation est de transmettre des signaux isolés. Le rapport de transformation est de 1, 2 ou 0,5. Il existe des version avec deux enroulements secondaires identiques.
Le problème déterminant est d'éviter la saturation du noyau magnétique. Les résistances de bobinage, les fuites magnétiques ont peu d'effet dans les applications. Le soin apporté au choix du matériau magnétique rend les pertes fer négligeables.
Modèle du transformateur d'impulsions
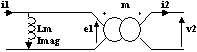
Exemple de structure utilisant un transformateur d'impulsions
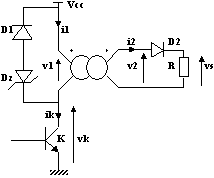
K travaille en commutation à la période T avec un rapport cyclique ![]() . Formes d'ondes :
. Formes d'ondes :
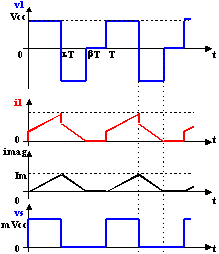
Justification des tracés :
De 0 à ![]() T
T
vk = 0 donc v1 = Vcc
Le courant magnétisant imag = (Vcc/Lm).t
Au secondaire v2 = m.Vcc est positive donc la diode D2 conduit et Vs = m.Vcc
Alors i2 = m.Vcc/R et i1 = m2.Vcc/R + (Vcc/Lm).t
A ![]() T
T
imag = Im = (Vcc/Lm).![]() T
T
De ![]() T à
T à ![]() T
T
Il y a du courant dans Lm avec D1 et Dz conductrice v1 = - Vz, imag = (-Vz/lm).(t-![]() T) + Im
T) + Im
Alors v2 = -m.Vz est négative ce qui bloque la diode D2. Donc vs = 0.
A ![]() T, le courant imag = 0 et les diodes se bloquent. v1 = v2 = 0, i1 = i2 = ik =0
T, le courant imag = 0 et les diodes se bloquent. v1 = v2 = 0, i1 = i2 = ik =0
Conditions de fonctionnement
- Il faut que
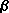 T < T
T < T
Dans le cas contraire, le courant magnétisant croît à chaque période jusqu'à la destruction d'un élément !
Il faut donc : (Vcc/Lm). T < (Vz/Lm).(T-
T < (Vz/Lm).(T- T) et
T) et  < Vz/(Vz + Vcc)
< Vz/(Vz + Vcc) - Il faut aussi éviter que Im sature le noyau magnétique du transformateur
(Im = (Vcc/Lm). T)
T)
Le constructeur connaît le courant Im maximum tolérable et Lm.
Comme Immaxi.Lm = Vcc. T, le constructeur donne un paramètre en V/µs qui correspond à (Vcc.
T, le constructeur donne un paramètre en V/µs qui correspond à (Vcc. T) maximum.
T) maximum.
Voir aussi :
Transformateur d'impulsion
Transformateur d'intensité