Ce frein à poudre est destiné à charger des moteurs d'une puissance nominale jusqu'à 1,5 KW à 1500 tr/mn

 Principe de fonctionnement du frein à poudre 

    Le frein à poudre est constitué d'un stator A (qui contient la bobine électromagnétique) et d'un rotor B (entraîné par le moteur en essai) concentriques. Lorsqu'on fait circuler un courant continu dans la bobine, un champ magnétique proportionnel à ce courant est créé. Ce champ traverse l'entrefer garni de poudre aux propriétés magnétiques et mécaniques particulières. Les grains de poudre forment alors des chaînes orientées entre A et B dont la rigidité est directement proportionnelle à l'intensité du courant traversant la bobine et qui engendrent un couple résistant

    Propriétés fondamentales du frein à poudre:

• le couple est proportionnel au courant
• pour un courant donné, le couple reste constant quelle que soit la vitesse

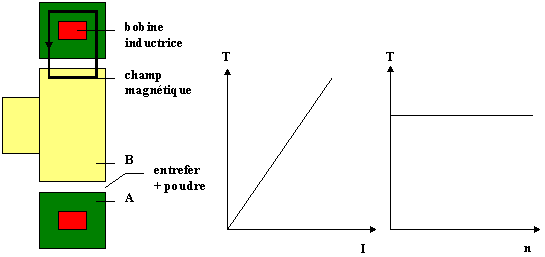
 Générateur de courant 

Il permet de maintenir le couple stable, indépendant des variations thermiques du frein

Cahier des charges:

• montage en coffret
• alimentation par réseau E.D.F. 230 v / 50 Hz
• courant réglable de 0 à 1A
• 4 moyens de réglage sélectionnés par commutateur en face avant
  • entrée extérieure tension 0 - 10 v
  • entrée extérieure courant 0 - 20 mA
  • entrée extérieure courant 4 - 20 mA
  • potentiomètre en face avant
• bornes de raccordement en face arrière
• interrupteur Marche/Arrêt avec voyant de signalisation
• signalisation du défaut " fil coupé " (4 - 20 mA)
• protection par fusible

   

  ---

  
   Générateur de courant 

Dans toute la suite: les AOP fonctionnent en linéaire (V+ = V-). Ils sont alimentés par une tension continue comprise entre 22v et 24v (monotension)

 1. Etage de puissance 

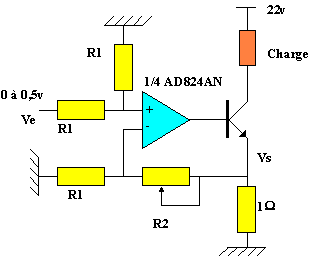
Pour une charge égale à 1A, Vs = 1 x 1 = 1v
V+ = Ve/2 = V- = Vs . R1 / (R1 + R2)
Vs = Ve (R1 + R2) / 2R1
On veut I(Charge) = 1A pour Ve = 0,5v
On prend R1=1k
R1 + R2 = 2R1 . Vs/Ve = 2 . 1/0,5 = 4 K
R2 = 3K
On prend R2 ajustable 4,7K ou 5K

 
 2. Atténuateur par 20 

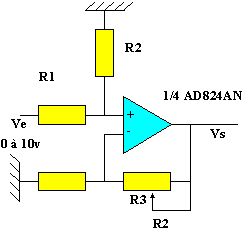
2.a. Expression de Vs en fonction de Ve, R1, R2 et R3:
V+ = Ve . R2 / (R1 + R2) = V- = Vs . R2 / (R3 + R2)
d'où: Vs = Ve (R3 + R2) / (R1 + R2)

2.b. On prend R2 = 1K
on veut G = 1/20 = 0,05
on prend R1 = 47K et R3 = 1K fixe + 1K ajustable
vérification: 2/48 = 0,041 < G < 3/48 = 0,062

 3. Convertisseur courant / tension 0 - 20 mA / 0 - 10 v 

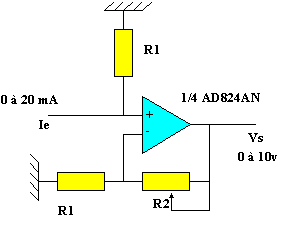
3.a. Expression de Vs en fonction de Ie, R1et R2:
V+ = R1 . Ie = V- = Vs . R1 / ( R1 + R2 )
d'où: Vs = (R1 + R2) Ie

3.b. On prend R1 = 47. Calcul de R2:
pour Ie = 20 mA, Vs = 10 v
R1 + R2 = 10 / 0,02 = 500
on prend R2 ajustable 470 ou 500

 
 4. Alimentation continue 

Cette alimentation doit fournir une tension redressée et filtrée de valeur Vmax=24v et Vmin=22v et un courant de 1 A à partir du réseau 230v-50Hz

Schéma

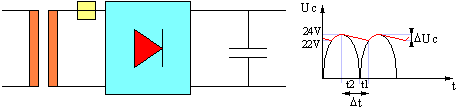
Puissance de sortie: P = 23 x 1 = 23W
Puissance apparente du transformateur: 35 à 46 VA. (1,5 à 2 fois P)
Tension secondaire: (24 + 1,4 (diodes) ) / 2 = 18v efficaces
Dimensionnement du condensateur :
On a une ondulation de tension de 2v avec Vmax = 24v et Vmin = 22v
Vmin = Vmax sin wt1 d'où t1 = 1/w * Arcsin (Vmin/Vmax) = 3,7 ms
i = C(dUc/dt) or i=constante=I
La décharge du condensateur étant linéaire : C=I (t/Uc)
t2 = 5 ms (1/4 de la période du réseau)
t = t1 + t2 = 8,7 ms
D'où: C= 4350 µF, soit en valeur normalisée : 4700 µF/40 v

 5. Convertisseur courant / tension 4 - 20 mA / 0 - 10v 

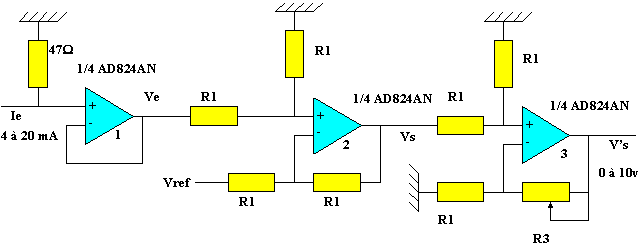
Calcul de Ve :
- pour 4 mA: V+ = 0,004 x 47 = 0,188 v = V- = Ve
- pour 20 mA: V+ = 0,02 x 47 = 0,94 v = V- = Ve

L' AOP n°1 présente une grande impédance d'entrée (suiveur) et ne prélève qu'une infime partie du courant Ie. L'AOP n°2 est un amplificateur différentiel. Les résistances R1 sont des résistances de précision

Calcul de Vs en fonction de Ve et Vref:
V+ = Ve / 2
V- = (Vs - Vref) / 2 + Vref = Ve / 2
Vs = 2 ( Ve/2 - Vref ) + Vref = Ve - Vref
Calcul de Vref:
- pour Ie=4mA | Vs=0 | Ve=0,188v | Vref=0,188v
- pour Ie=20mA | Ve=0,94v | Vref=0,188v | Vs=0,752v
Calcul de V's en fonction de Vs, R1, R3:
V+ = Vs / 2 = V- = V's R1 / (R1+R3)
V's = Vs (R1+R3)/2R1
On prend R1=1K
Détermination de R3 :
20/0,752 = 26,6 -> R3=25,6K
On prend R3 ajustable 47K

 6. Référence de tension 

La tension Vref est élaborée à partir du circuit TL 431 (référence de tension de précision)

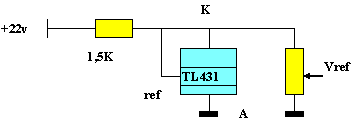
 7. Signalisation " fil coupé " 

 
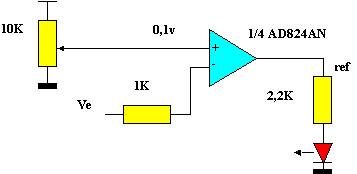
 8.Synoptique 

 

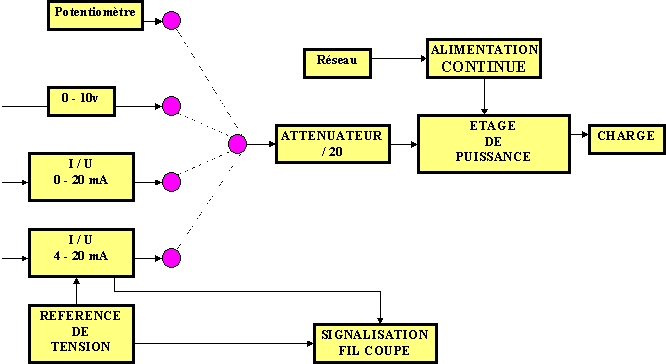
 9. Puissance dissipée dans le transistor 

On suppose que l'alimentation continue ( voir 4 ) fournit une tension parfaitement constante égale à V = 24 v. La résistance de la bobine du frein à poudre est R = 20 . On néglige l'influence du shunt ( 1 )
Calcul de la puissance maximale dissipée dans le transistor:
Vce = V - R . I et P = Vce . I = V . I - R . I²
La puissance est maximale lorsque la dérivée de P par rapport à I devient nulle
0 = V - 2 . R . I
I = V / (2 . R) = 24 / 40 = 0,6A
Vce = 24 - 20 x 0,6 = 12v
P = 12 x 0,6 = 7,2W
Choix du dissipateur pour le TIP 121:
TIP 121: Vce=80v Ic=5A P=65W =1000
Pd=T(v-j)max - Tamb / Rth(r-amb) =
Pd=T(v-c)max - T amb / Rth(j-c) + Rth(c-r) + Rth(r-amb)
Pd= puissance dissipée
T(v-j)max= température de jonction maximale
Tamb= température ambiante
Rth(j-c)= résistance thermique jonction - boîtier
Rth(c-r)= résistance thermique boîtier - dissipateur
Rth(r-amb)= résistance thermique dissipateur - ambiance
Tc= température boîtier
Tr= température dissipateur

Rth(c-r) du T 220

• 1,4 direct
• 0,3 °C/W avec graisse thermoconductrice
• 2,2 °C/W avec isolant
• 0,8 °C/W avec isolant + graisse thermoconductrice

Rth(r-amb) = [T(v-j)max - Tamb / Pd] - [Rth(j-c) + Rth(c-r)]
On a :
Pd = 7,2 W
T(v-j)max = 150°C
Tamb = 40°C
Rth(c-r) = 1,4 (donné par le fabricant)
Rth(j-c) = 2 (donné par le fabricant)
Rth(j-c) = 2°C/W
Rth(j-amb) = 70°C/W
Rth(r-amb) = [ (150 - 40) / 7,2 ] - [ 2 + Rth(c-r) ]

Fonctionnement normal:
Pour Rth(c-r) =1,4 (direct) on a : Rth(r-amb) = 11,88 °C/W
0,5 °C/W (avec graisse) Rth(r-amb) = 12,78 °C/W
2,2 °C/W (avec isolant) Rth(r-amb) = 11,08 °C/W
0,8 °C/W (avec graisse + isolant) Rth(r-amb) = 12,48 °C/W

Fonctionnement en court-circuit :
V=Vce et I=1 A
P = Vce * I P = 24 W
On a :
Rth(r-amb) = 1,18 °C/W
Rth(r-amb) = 2,08 °C/W
Rth(r-amb) = 0,38 °C/W
Rth(r-amb) = 1,78 °C/W

Les calculs nous proposent donc un dissipateur pour un fonctionnement dans le cas le plus défavorable, c'est à dire en court-circuit : Rth(r-amb) = 0,38 °C/W

On a donc le choix entre deux dissipateurs aluminium anodisé (d'après SCHAFFNER) :
-WA 207 (longueur :124 mm ; largeur :72 mm ; poids :11,07 kg/m)
-WA 290 (longueur :125 mm ; largeur :81,2 mm ; poids :8 kg/m)

On constate que les dissipateurs sont beaucoup trop volumineux pour l'application à laquelle on les destine (dimensions du dissipateur trop importantes par rapport à celles du boîtier). On fixera donc le transistor sur le boîtier du générateur de courant en prenant soin de l'isoler électriquement de celui-ci grâce à une rondelle de mica. La carcasse de ce boîtier étant suffisante pour dissiper la puissance engendrée par le transistor