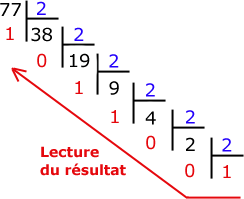
77 en décimal se décompose en 64 + 8 + 4 + 1 ce qui donne 1001101 en binaire après décalage vers la droite 100110 ... 1 (reste) ce qui donne 32 + 0 + 0 + 4 + 2 + 0 = 38 ... reste 1

La division par 2 ne pose aucun problème : il suffit d'effectuer un décalage vers la droite

23 22 21 20 1 1 0 0

= 23 x 1 + 22 x 1 + 21 x 0 + 20 x 0 = 12

divisé par 2 (décalage vers la droite)

23 22 21 20 0 1 1 0

= 23 x 0 + 22 x 1 + 21 x 1 + 20 x 0 = 6

divisé par 2 (décalage vers la droite)

23 22 21 20 0 0 1 1

= 23 x 0 + 22 x 0 + 21 x 1 + 20 x 1 = 3

---

La division par un entier quelconque est plus complexe

Soit à diviser 12 par 6

Le dividende est codé sur 2 quartets

Dividende		Diviseur	Quotient
23 22 21 20 0 0 0 0	23 22 21 20 1 1 0 0	23 22 21 20 0 1 1 0	23 22 21 20 0 0 0 0

1. Décalage à gauche du Dividende et du Quotient

Dividende		Diviseur	Quotient
23 22 21 20 0 0 0 1	23 22 21 20 1 0 0 0	23 22 21 20 0 1 1 0	23 22 21 20 0 0 0 0

Comparaison Dividende (poids forts) et Diviseur : 1 < 6

2. Décalage à gauche du Dividende et du Quotient

Dividende		Diviseur	Quotient
23 22 21 20 0 0 1 1	23 22 21 20 0 0 0 0	23 22 21 20 0 1 1 0	23 22 21 20 0 0 0 0

Comparaison Dividende (poids forts) et Diviseur : 3 < 6

3. Décalage à gauche du Dividende et du Quotient

Dividende		Diviseur	Quotient
23 22 21 20 0 1 1 0	23 22 21 20 0 0 0 0	23 22 21 20 0 1 1 0	23 22 21 20 0 0 0 0

Comparaison Dividende (poids forts) et Diviseur : 6 = 6

Calcul du nouveau Dividende = Dividende (poids forts) - Diviseur
et incrémentation du Quotient

Dividende		Diviseur	Quotient
23 22 21 20 0 0 0 0	23 22 21 20 0 0 0 0	23 22 21 20 0 1 1 0	23 22 21 20 0 0 0 1

4. Décalage à gauche du Dividende et du Quotient

Dividende		Diviseur	Quotient
23 22 21 20 0 0 0 0	23 22 21 20 0 0 0 0	23 22 21 20 0 1 1 0	23 22 21 20 0 0 1 0
			Résultat = 2

---

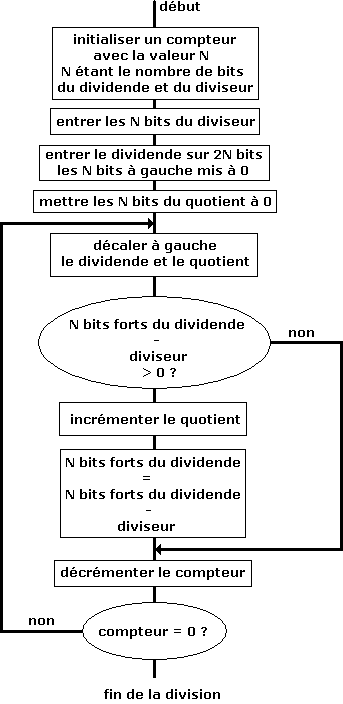
En généralisant cette démarche à N bits

1. Le Diviseur contient N bits
   Le Quotient contient N bits tous mis à 0
   Le Dividende contient N bits (poids faibles) et N bits à gauche (poids forts) mis à 0
2. Décalage à gauche du Dividende et du Quotient
3. Comparaison du Dividende (poids forts) et du Diviseur
   Si Dividende >= Diviseur : incrémentation du Quotient et calcul du nouveau Dividende
4. Répétition N fois des opérations 2 et 3

---

Autre exemple : diviser 15 par 3

Dividende		Diviseur	Quotient
23 22 21 20 0 0 0 0	23 22 21 20 1 1 1 1	23 22 21 20 0 0 1 1	23 22 21 20 0 0 0 0

1. Décalage à gauche du Dividende et du Quotient

Dividende		Diviseur	Quotient
23 22 21 20 0 0 0 1	23 22 21 20 1 1 1 0	23 22 21 20 0 0 1 1	23 22 21 20 0 0 0 0

Comparaison Dividende (poids forts) et Diviseur : 1 < 3

2. Décalage à gauche du Dividende et du Quotient

Dividende		Diviseur	Quotient
23 22 21 20 0 0 1 1	23 22 21 20 1 1 0 0	23 22 21 20 0 0 1 1	23 22 21 20 0 0 0 0

Comparaison Dividende (poids forts) et Diviseur : 3 = 3

Calcul du nouveau Dividende = Dividende (poids forts) - Diviseur
et incrémentation du Quotient

Dividende		Diviseur	Quotient
23 22 21 20 0 0 0 0	23 22 21 20 1 1 0 0	23 22 21 20 0 0 1 1	23 22 21 20 0 0 0 1

3. Décalage à gauche du Dividende et du Quotient

Dividende		Diviseur	Quotient
23 22 21 20 0 0 0 1	23 22 21 20 1 0 0 0	23 22 21 20 0 0 1 1	23 22 21 20 0 0 1 0

Comparaison Dividende (poids forts) et Diviseur : 1 < 3

4. Décalage à gauche du Dividende et du Quotient

Dividende		Diviseur	Quotient
23 22 21 20 0 0 1 1	23 22 21 20 0 0 0 0	23 22 21 20 0 0 1 1	23 22 21 20 0 1 0 0

Comparaison Dividende (poids forts) et Diviseur : 3 = 3

Calcul du nouveau Dividende = Dividende (poids forts) - Diviseur
et incrémentation du Quotient

Dividende		Diviseur	Quotient
23 22 21 20 0 0 0 0	23 22 21 20 0 0 0 0	23 22 21 20 0 0 1 1	23 22 21 20 0 1 0 1
			Résultat = 5

---

Algorithme de programmation