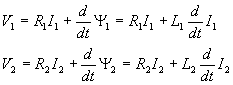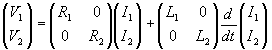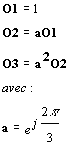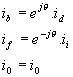Ce document est un essai de synthèse sur les transformations des systèmes de grandeurs triphasées utilisées dans l'étude des machines électriques. Ces transformations étaient à l'origine (premier quart du 20ième siècle) destinées à la simplification des calculs par l'établissement d'un schéma monophasé en remplacement des 3 phases magnétiquement couplées.
Malgré l'arrivée de moyens de calcul permettant de traiter directement les équations triphasées, ces transformations n'ont pas perdu leur intérêt dans la mesure où le schéma monophasé qui en est issu permet une meilleure compréhension des phénomènes et que leur usage fait apparaître des grandeurs directement utilisables dans le domaine de la commande des machines.
On présente rapidement, comme exemple, les équations de description d'une machine asynchrone, puis on essaye de mettre en évidence les bienfaits apportés par les différentes transformations.
Plan du document :
ÉQUATIONS DE LA MACHINE ASYNCHRONE
(juste pour se rendre compte)
détails, voir : Philippe Barret, régimes transitoires des machines tournantes électriques Eyrolles
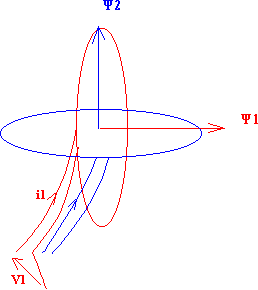
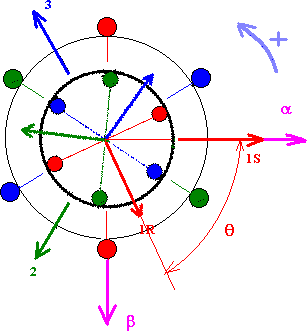
Ci - dessous la représentation schématique d'une machine triphasée munie d'une armature statorique comportant trois enroulements triphasés dont les axes sont décalés de 120°, on se sert de l'axe de la phase statorique 1S pour repérer les angles (on aurait pu prendre un axe arbitraire quelconque), en particulier l'angle stator - rotor q :
Sous réserve de certaines hypothèses ( machine non saturée, répartition sinusoïdale du flux sur la périphérie d'entrefer ), on peut définir les inductances propres et mutuelles au stator et au rotor, ainsi que les mutuelles entre enroulements statoriques et rotoriques.
Dans ces conditions, les relations liant les flux d'enroulement et les courants des différentes phases peuvent s'écrire :
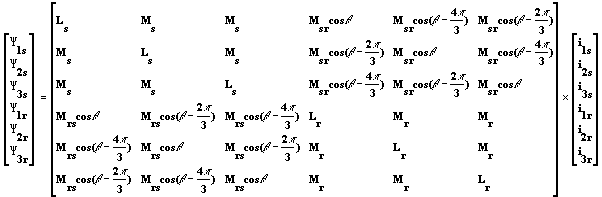
- 1, 2, 3, sont les numéros de phases statoriques ou rotoriques, s pour stator, r pour rotor
- on suppose que le rotor possède trois phases
- l'angle q est l'angle formé par les axes de deux phases statoriques et rotoriques homologues ( e.g entre 1s et 1r )
La vitesse de rotation de la machine est alors :
![]()
En raison de la symétrie de la machine, on a :
![]()
Ne serait-ce que pour les relations flux/courants, on a affaire à un système de six équations.
Il manque les relations électriques (tensions /courants statoriques et rotoriques, encore six équations) :
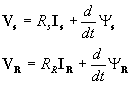
et les relations électromécaniques (couple/vitesse et couple/courants, flux) :
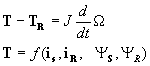
soit au total quatorze équations où toutes les grandeurs sont liées ( voyez le travail!).
On va essayer de se le simplifier : pour cela, on va entreprendre l'étude de certaines transformations permettant le découplage (total ou partiel) de toutes ces grandeurs (surtout en ce qui concerne les relations flux/courants).
TRANSFORMATIONS DES SYSTÈMES TRIPHASÉS
La philosophie de l'étude suivante repose sur deux points de vue, l'un mathématique, l'autre physique, mais tous deux équivalents :
- la diagonalisation de la matrice flux/courants : on cherche une base de vecteurs dans laquelle les équations décrivant le fonctionnement d'une machine électrique soient découplées, c'est à dire que les grandeurs relatives à une phase ne dépendent pas des autres phases (en particulier de leur flux); les matrices liant les différentes grandeurs sont alors diagonales. La base répondant à ces préoccupations étant trouvée, la difficulté est ensuite d'interpréter physiquement les grandeurs qui la composent (le courant dans une phase, on "voit" ce que c'est, un courant d'axe q beaucoup moins...)
- l'extension du théorème de BLONDEL (André 1863-1938) qui permet de remplacer un système triphasé par un système diphasé équivalent (en termes de champs tournants). En effet, entre deux enroulements dont les axes présentent un écart angulaire de 90°, les flux mutuels sont nuls, d'où disparition des termes hors diagonale de la matrice flux/courants :
|
|
|
|
DIAGONALISATION DE LA MATRICE "INDUCTANCE"
TRANSFORMATION DE FORTESCUE
Pour une armature statorique ou rotorique (mais sans interaction entre les deux, le " ou " précédent étant à prendre au sens exclusif du terme), la matrice flux/courants s'écrit :
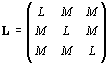
Cette matrice possède trois valeurs propres qui sont :
(en cas, voir rappels de maths)
l = L - M(double) et l = L + 2M
Les coordonnées des vecteurs propres X,Y,Z associés doivent vérifier les relations suivantes :

Une solution possible en nombres complexes est :
X1 = 1, X2 = a2, X3 = a
Y1 = 1, Y2 = a, Y3 = a2
Z1 = Z2 = Z3 = 1
On vérifie facilement que X, Y et Z sont linéairement indépendants, on peut donc les choisir comme nouvelle base.
La matrice de passage correspondante, définit la transformation de Fortescue :
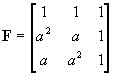
La matrice diagonale s'écrit :
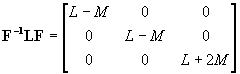
Les trois valeurs non nulles de cette matrice définissent les inductances cycliques de l'armature triphasée.
TRANSFORMATIONS TRIPHASÉES/DIPHASÉES
TRANSFORMATION DE CLARKE
On cherche à exprimer les différentes relations initialement écrites dans le système d'axes (O1,O2,03) dans le système (Oa,Ob).
Ici, on a choisi l'axe Ob en retard sur l'axe Oa . Cela présente un intérêt dans l'étude de la machine synchrone dans la mesure où, le flux inducteur étant sur un axe, les fém. induites se trouvent selon l'axe en quadrature arrière.
Certains auteurs(J. Chatelain, Hauthier-Caron) préfèrent utiliser un système tel que, en ajoutant un axe pour la composante homopolaire, ce système forme un trièdre direct (mais dans la mesure où il est difficile de parler de trièdre pour le système (O1,O2,O3)...). Cela conduit à un changement de signe dans la deuxième ligne des transformations.
On suppose d'abord l'angle q = 0
En supposant les vecteurs unitaires, et en prenant l'axe de l'enroulement 1 comme axe des réels, on a les relations suivantes entre les vecteurs directeurs des différents axes :
|
|
On cherche alors la transformation C telle que :
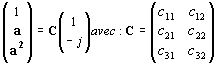
En identifiant, on trouve les relations :
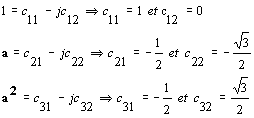
pour des grandeurs x quelconques (flux, courants, tensions, etc...) on a donc :
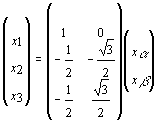
Par cette transformation on peut vérifier que :
![]()
Elle ne convient pas pour un système présentant une composante homopolaire non nulle. On adjoint alors une troisième colonne de telle sorte que la composante homopolaire X0 soit égale à la somme des trois grandeurs X1,X2,X3
On obtient, de cette façon, la transformation de Miss Edith CLARKE :
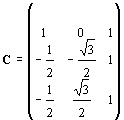
Cette transformation diagonalise bien la matrice L (flux/courants) (elle l'a construite pour ça, entre autres), et on obtient dans le système (a,b,0) :
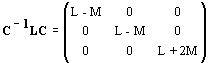
avec :
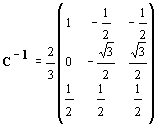
EXPRESSION DES GRANDEURS ELECTROMAGNETIQUES
APRÈS TRANSFORMATION DE CLARKE
on peut écrire les relations ( flux, courants ) sous la forme (dans le système ( 1,2,3 ) :
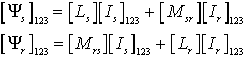
en appliquant la transformation de Miss CLARKE, on obtient dans le système (a,b,0) :
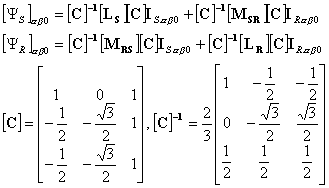
tous calculs faits, on arrive à : ( toujours dans (a,b,0) )
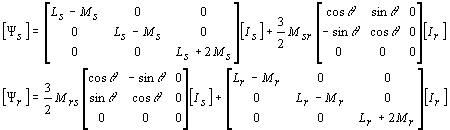
Les relations flux/courants ne sont pas encore découplées à cause de la matrice :
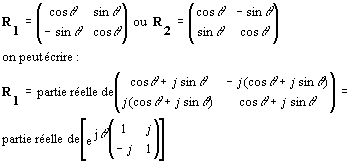
Pour simplifier encore, on peut chercher à diagonaliser cette dernière matrice :
Pour celle-ci, les valeurs propres sont : l = 0 et l = 2
Deux vecteurs propres possibles (et il y en a d'autres, mais la solution suivante ne manque pas d'intérêt) sont :
![]()
où d et e sont des réels quelconques. Les deux vecteurs sont orthogonaux, on peut normer la matrice de passage en divisant chacun d'eux par sa propre norme. On obtient alors la matrice de passage suivante :
![]()
La matrice inverse vaut :
![]()
La diagonalisation de R1 donne :
![]()
et celle de R2 :
![]()
De plus, la transformation P laisse inchangées les matrices de type L. Les relations flux/courants dans le nouveau système qu'on baptise (a', b', o') s'écrivent alors (compte non tenu de la composante homopolaire) :
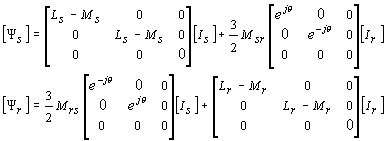
REMARQUE : on remarquera, non sans aisance, que le produit de la transformation de Miss CLARKE par la matrice de passage P donne la transformation de Fortescue :
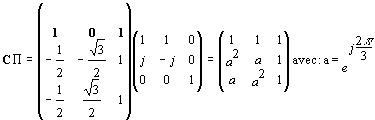
TRANSFORMATION DE PARK
Les relations flux/courants sont maintenant entièrement découplées, cependant il reste encore la dépendance avec l'angle q, c'est à dire, pour une machine tournante la dépendance avec le temps.
On peut alors envisager de modifier la transformation de Miss CLARKE en supposant les axes (Oa, Ob) décalés d'un angle q par rapport à l'axe de la phase 1 (qui nous sert de références, voir figure) ; on baptise les nouveaux axes (Od, Oq) nommés respectivement axe direct et axe en quadrature.
On passe du système (a,b,0) au système (d,q,0) par application d'une simple rotation d'angle q autour de l'axe Oz (voir figure) :
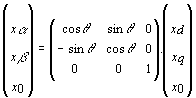
en effectuant le produit des 2 matrices (donc le produit des 2 transformations) on obtient la transformation de Monsieur PARK :

TRANSFORMATION DE KU
La transformation de Monsieur PARK, si elle permet de s'affranchir de la dépendance des relations en ce qui concerne l'angle q, ne permet pas le découplage total de celles-ci.
Tiens, si on appliquait la transformation P déjà utilisée plus haut ?
Le résultat donne la transformation de Y.H. KU : K = PP
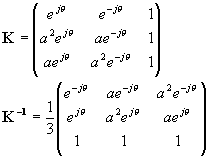
Transformation des grandeurs électriques par la transformation de Monsieur KU .
Si on baptise les coordonnées issues de cette dernière transformation par (xb, xf, x0),
on a, par exemple, pour un courant :
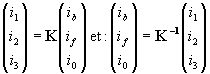
On a alors :
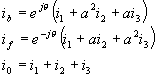
On s'aperçoit, que les composantes(b, f, 0) sont apparentées aux composantes symétriques (d, i, 0) issues de la transformation de Fortescue :
RÉSUMÉ
passage du système (1,2,3) au système (direct, inverse, homopolaire) = (d,i,0)
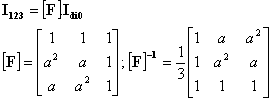
passage de (1,2,3) à (a,b,0)
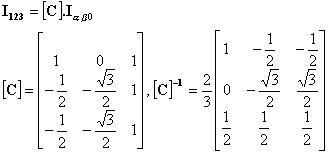
passage de (1,2,3) à (direct, quadrature, homopolaire)=(d,q,0)
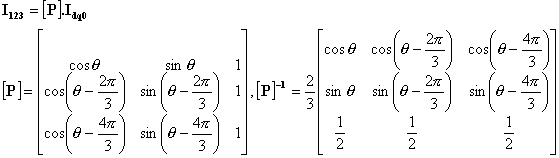
passage de (1,2,3) à (b,f,0)
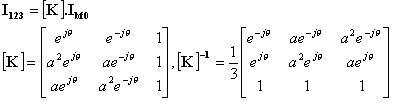
RELATIONS ENTRE LES
Transformations de Clarke et de Fortescue
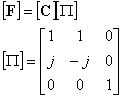
Transformations de Clarke et de Park
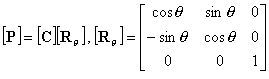
Transformations de Ku et de Park
![]()
Composantes de Ku et composantes symétriques
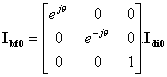
Voila, c'est fini, merci !
On rappelle que les valeurs propres l d'une application linéaire f de matrice L sont telles que pour un vecteur V on a :

Les vecteurs V vérifiant cela sont appelés vecteurs propres. Dans la base des vecteurs propres (si elle existe) la matrice de l'application f est alors diagonale, les valeurs de cette diagonale étant les valeurs propres elles mêmes.
Dans notre cas :
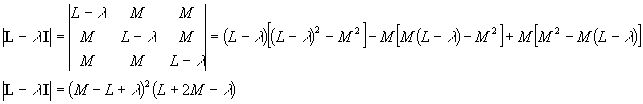
Pour la valeur propre l = L-M qui est une solution double, il y a 2 vecteurs propres associés définissant un sous espace vectoriel de dimension 2 (un plan en français) :
Ils sont tels que :
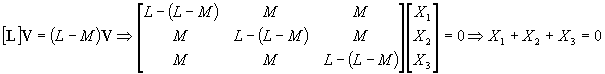
On doit donc trouver 2 vecteurs X et Y linéairement indépendants, dont les coordonnées vérifient :
![]()
Pour la valeur propre l = L+2M :
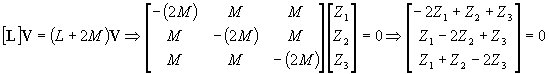
On en déduit :
![]()