1- Définition 

    Un quadripôle est une structure électronique dont on considère l'entrée entre deux bornes et la sortie entre deux bornes. Les signaux électriques en entrée et en sortie peuvent être de nature différente (tension, courant, puissance ).

 2- Caractérisation d'un quadripôle 

 2.1 Symbolisation d'un quadripôle 

    Le quadripôle est représenté par un rectangle avec généralement ses deux bornes d'entrée à gauche et ses deux bornes de sortie à droite. Les signaux électriques en entrée et en sortie sont reportés sur les liaisons d'entrée et de sortie. Si par exemple l'étude porte sur une structure électronique qui opère sur une entrée en tension et une sortie en tension :

 2.2 Fonction de transfert d'un quadripôle 

    Les fonctions électroniques traitent les signaux électriques dans un vaste champ de fréquence, de zéro à plusieurs dizaines de giga hertz. Pour caractériser la fonction opérée par la structure électronique sur le signal, il faut donc un paramètre qui permette de connaître précisément quel est le signal de sortie pour une entrée donnée. Et cela à toutes les fréquences. 
    C'est la fonction de transfert du quadripôle telle que T = Vs / Ve , avec un courant de sortie nul.

 2.3 Impédance d'entrée d'un quadripôle 

    Le modèle équivalent du quadripôle vu des bornes d'entrée se réduit dans la plupart des cas à une impédance, c'est l'impédance d'entrée Ze du quadripôle. En général l'impédance d'entrée considère une sortie chargée.

 2.4 Impédance de sortie d'un quadripôle 

    Le modèle de Thévenin équivalent à la sortie du quadripôle comporte un générateur de tension tel que T . Ve en série avec une impédance Zs, cette dernière est l'impédance de sortie du quadripôle.

 2.5 Modèle équivalent au quadripôle 

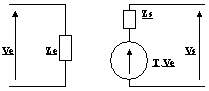
 3- Diagrammes de Bode 

    Pour identifier aisément la fonction remplie par le quadripôle à toutes les fréquences, il convient de faire une représentation graphique du module de T et de sa phase en fonction de la fréquence ou de la pulsation des signaux.
    Compte tenu de la grande étendue des valeurs du module de T, on préfère tracer la fonction : G = 20 log | T | en fonction de la fréquence ou de la pulsation des signaux. G s'appelle le gain de la fonction de transfert T et s'exprime en décibels (dB).
    De même les fréquences sont considérées dans une plage très étendue de valeurs. Les tracés des diagrammes de Bode sont finalement :

• pour l'amplitude de T , G = f(w) où la pulsation w est portée en échelle logarithmique
• pour la phase de T , Arg T = f(w) où la pulsation w est portée en échelle logarithmique

    Notion de bande passante : 
soit le tracé suivant de G = f(w)

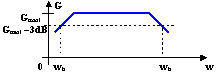
w_h-w_b = bande passante à -3dB

 4- Exemple 

    Soit le quadripôle élémentaire suivant :

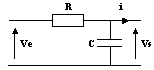
    Le calcul de la fonction de transfert pour i = 0 donne T = Vs / Ve = 1 / 1 + jRCw. On en déduit :

• le gain associé G = -10log[1 + (RCw)²]
• la phase Arg T = -arctg RCw

    Pour faire le tracé des diagrammes de Bode il faut faire une étude préalable des fonctions G et Arg T = f(w).

Lim _{w-> æ} G » - æ  

Mais la fonction G = f(w) tend vers G = -20logRCw = 20logw + 20logRC 
Cette dernière forme de G = f(w) correspond à une fonction affine dans un repère où les abscisses sont en échelle logarithmique.  
C'est la tangente à la fonction G = f(w) quand w tend vers l'infini. Elle porte le nom de direction asymptotique pour les très fortes valeurs de w. Cette droite passe par G = 0 pour w = 1/RC et présente une pente de -20dB par décade.

Lim _{w-> 0} G » 0

Pour les faibles valeurs de w la fonction G = f(w) tend vers une fonction affine d'équation 0 
C'est la direction asymptotique de G = f(w) pour les faibles valeurs de w.

Remarquons pour la valeur particulière w₀ = 1/RC, G = G_maxi-3dB
Donc w₀ =1/RC est une pulsation de coupure à -3dB du quadripôle.

Lim _{w-> æ} Arg T » -90°
Lim _{w-> 0} Arg T » 0
Pour w = w₀ Arg T = -45°

Tracé des diagrammes de Bode asymptotiques :

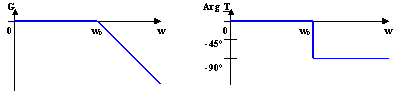
    Sur le tracé du gain la courbe réelle se situe à 3 dB du tracé asymptotique 
pour w = w₀ et se rapproche à 1dB pour w = w₀/2 et 2w₀. 
    Le tracé asymptotique est souvent suffisant pour caractériser la réponse du quadripôle.

    L'observation du tracé du gain G = f(w) permet de caractériser la réponse du quadripôle vis à vis de la pulsation des signaux. 
    Dans l'exemple ci-dessus il s'agit d'un " filtre passe bas ".

    La bande passante à -3dB du quadripôle s'étend de 0 à w₀

Exercices