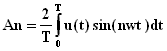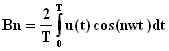1- Décomposition en série de Fourrier d'un signal
Un signal périodique u(t) de période T est équivalent à une somme infinie de termes :
![]()
où:
|
|
|
Ainsi tout circuit électrique soumis à un signal non sinusoïdal mais périodique répond à un spectre infini de termes sinusoïdaux plus éventuellement une composante continue.
La notation complexe est utilisable pour les composantes sinusoïdales et le théorème de superposition s'applique pour l'étude.
Un quadripôle qui élimine une partie des signaux du spectre s'appelle un filtre.
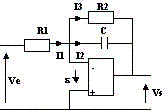
2- Filtre passe bas
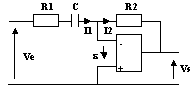
Dans l'hypothèse de l'ALI parfait : I1 = I2 + I3 et e = 0
Ve = R1.I1
Vs = -I2/jCw
Vs = -R2.I3
T = Vs / Ve = -(R2/R1).1 / (1+jR2Cw)
Le gain associé:
G = 20 log(R2/R1) - 10log[1+(R2Cw)2].G0 = 20log(R2/R1) et w0 = 1/R2C
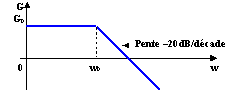
Réponse en fréquence du quadripôle
Le comportement est celui d'un filtre passe bas du premier ordre. " Passe bas " car les composantes de pulsation inférieure à w0 sont transmises avec un gain G0, alors que celles dont la pulsation est supérieure sont affaiblies. " premier ordre " car la pente du diagramme asymptotique est de -20dB par décade.
3- Filtre passe haut
Dans l'hypothèse de l'ALI parfait : I1 = I2 et e = 0
Ve = (R1 + 1/jCw).I1
Vs = -R2.I1
T = Vs/Ve = -jR2Cw / (1 + jR1Cw)
Le gain associé:
G = 20 log(R2Cw) - 10log[1+(R1Cw)2].G0 = 20log(R2/R1) avec w0 = 1/R2C et w1 = 1/R1C
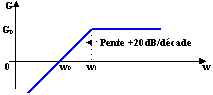
Réponse en fréquence du quadripôle
Le comportement est celui d'un filtre passe haut du premier ordre. " Passe haut " car les composantes de pulsation supérieure à w1 sont transmises avec un gain G0, alors que celles dont la pulsation est inférieure sont affaiblies. " premier ordre " car la pente du diagramme asymptotique est de +20dB par décade.
Notons qu'avec un ALI réel aux fréquences élevées le filtre présente aussi une coupure haute et en fait se comporte en passe bande.
4- Filtre passe bande
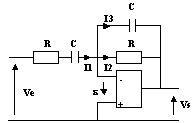
Dans l'hypothèse de l'ALI parfait : I1 = I2 + I3 et e = 0
Ve = (R + 1/jCw).I1
Vs = -I3/jCw
Vs = -R.I2
T = Vs / Ve = -jRCw/[(1 + jRCw).(1+jRCw)]
Le gain associé:
G = 20 log(RCw) -20log[1+(RCw)2]. Soit w0 = 1/RC
Réponse en fréquence du quadripôle
Le comportement est celui d'un filtre passe bande du premier ordre. " Passe bande " car les composantes de pulsation à w0 sont transmises avec un gain maximum alors que celles dont la pulsation est inférieure ou supérieure sont affaiblies. " premier ordre " car la pente du diagramme asymptotique est de +20dB par décade et -20 dB par décade.
Notons que la valeur du gain maximum à w0 est de -6dB.