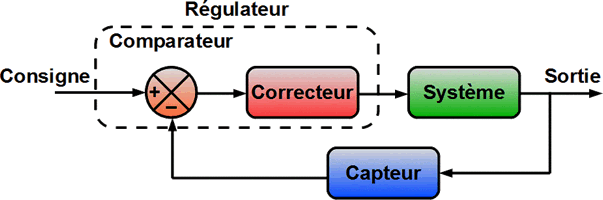
1. Système asservi
Un système linéaire est défini par des équations différentielles à coefficients constants. On peut associer à ces équations des fonctions de transfert exprimées en utilisant la notation complexe ou les transformées de Laplace (jw = p)
1.1. Principe
Schéma du système en boucle fermée :
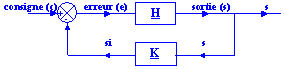
On souhaite asservir la variable de sortie s à la variable d'entrée c.
La variable d'entrée est appelée consigne : elle correspond à l'image de la valeur souhaitée en sortie.
L'erreur e est la différence entre la consigne c et l'image si de la sortie s. L'idéal serait que l'erreur e soit nulle pour que la sortie s suive fidèlement les valeurs de c.
Le système est équivalent à une fonction de transfert d'entrée c et de sortie s.
Le système comprend un mélangeur qui élabore l'erreur, une chaîne d'action H et une chaîne de retour K.
1.2. Schéma à retour unitaire

La sortie du schéma fonctionnel est l'image si de la sortie s.
1.3. Fonction de transfert du système en boucle fermée
A partir du schéma bloc du 1.1.
S = H.E = H.( C - K.S )
T = S /C = H / ( 1+K.H)
Remarque :
Si K.H = -1 le module de T tend vers l'infini.
Alors la sortie S existe à la pulsation w telle que K.H = -1 avec une certaine amplitude tandis que l'entrée c ne varie pas !
Il y a donc oscillation du système à la pulsation w. On dit que le système est instable. Cette situation est contraire à l'objectif d'un système asservi car s n'est plus contrôlée par c.
2. Degré de stabilité d'un système bouclé
Pour s'assurer que le système asservi est stable il faut considérer le produit K.H et vérifier qu'il existe une marge suffisante entre K.H et -1. Dans la majorité des applications il est nécessaire de corriger H en ajoutant une fonction de transfert dans l'électronique de commande. La fonction à insérer porte le nom de correcteur du système asservi.
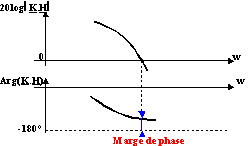
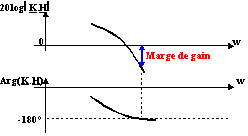
La stabilité du système est d'autant plus grande que K.H est différent de -1. Il s'agit donc de respecter une marge sur le module ou le gain de K.H et sur sa phase par rapport à -1.
L'expérience montre qu'une marge de 45° à 65° sur la phase ou bien une marge de 8 à 10dB sur le gain assurent une stabilité satisfaisante.
La marge de phase est égale à ![]() + Arg(K.H) pour la pulsation qui donne G = 0
+ Arg(K.H) pour la pulsation qui donne G = 0
La marge de gain est égale à -20 log| K.H | pour la pulsation qui permet d'obtenir arg(K.H) = -![]()
2.1. Caractérisation de la réponse d'un système asservi
Réponse à un échelon
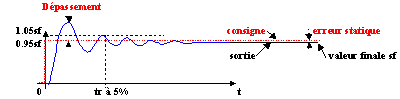
Soumis à un échelon ou la consigne varie de 0 à une valeur donnée, le système répond avec un dépassement exprimé en % de la valeur finale sf , un temps de réponse tr et une éventuelle erreur statique.
Réponse à une rampe

Quand la consigne est une rampe, la sortie peut suivre avec un retard constant : l'erreur de traînage est le paramètre qui caractérise cette réponse.
Le diagramme de Bode tracé en fonction de w nous renseigne sur la réponse du système : la réponse aux pulsations élevées correspond à la réponse en régime transitoire. De la réponse aux faibles pulsations on peut déduire la précision en régime permanent (erreur statique).
2.2. Exemples de réponse d'un système asservi
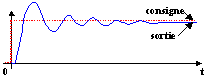
Cas où la marge de phase est trop faible
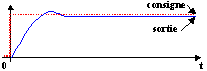
Cas d'une marge de phase de 45°
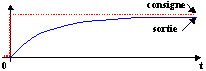
Cas d'une très forte marge de phase
2.3. Dilemme stabilité - précision
L'erreur sur la sortie d'un système asservi est ![]() s = limw-> 0 |S / H|. Pour améliorer la précision il suffit d'augmenter |H| de H0 quand w -> 0. Mais la marge de phase se réduit et la stabilité du système se dégrade :
s = limw-> 0 |S / H|. Pour améliorer la précision il suffit d'augmenter |H| de H0 quand w -> 0. Mais la marge de phase se réduit et la stabilité du système se dégrade :
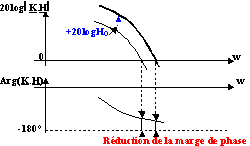
Rares sont les applications où il suffit d'augmenter le gain pour obtenir une précision convenable tout en conservant un bon niveau de stabilité. Il faut en général faire une correction plus sophistiquée qui évolue en fonction de la pulsation.
3. Correction d'un système du deuxième ordre
Soit un système du 2ème ordre tel que K.H = T = T0 / (1+j.![]() e.w)(1+j.
e.w)(1+j.![]() m.w). On veut déterminer le correcteur Hc qui permet d'obtenir la réponse attendue du système en matière de précision et de stabilité. Celui ci est inséré dans la chaîne d'action.
m.w). On veut déterminer le correcteur Hc qui permet d'obtenir la réponse attendue du système en matière de précision et de stabilité. Celui ci est inséré dans la chaîne d'action.

3.1. Pour une précision inchangée et une augmentation de la stabilité
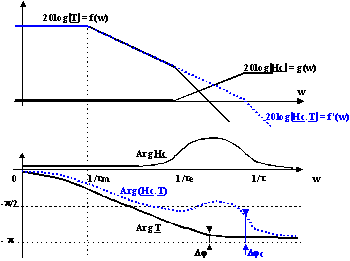
Dans cet exemple le correcteur ne modifie pas les diagrammes aux faibles pulsations. La précision est inchangée.
Par contre la marge de phase est améliorée de 30° à 60°. La stabilité est donc meilleure.
Le correcteur avance la phase dans le domaine des pulsations où il faut augmenter la marge de phase.
Il faut Hc = (1+j.![]() e.w)/(1+j.
e.w)/(1+j.![]() m.w). Pour 1/
m.w). Pour 1/![]() m < w < 1/
m < w < 1/![]() e , Hc ~ 1+j.
e , Hc ~ 1+j.![]() m.w et ec = e +
m.w et ec = e + ![]() de/dt.
de/dt.
L'action du correcteur est proportionnelle et dérivée " P.D ".
Conclusion :
Si la précision est satisfaisante on améliore le degré de stabilité par un correcteur en cascade de type proportionnel et dérivé.
Exemple de réalisation :
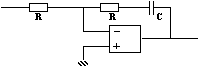
3.2. Pour augmenter la précision sans changer le degré de stabilité
Il faut augmenter le gain aux faibles pulsations sans modifier aux fortes pulsations.
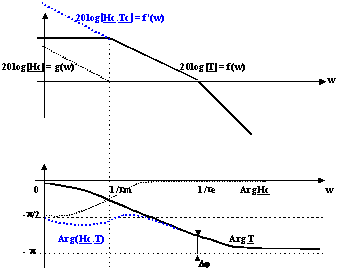
Ici Hc = (1+j.![]() m.w) / j.
m.w) / j.![]() m.w et aux faibles pulsations |Hc| tend vers l'infini.
m.w et aux faibles pulsations |Hc| tend vers l'infini.
L'erreur de régime permanent est donc nulle.
La marge de phase est inchangée.
Le correcteur intégral produit le signal d'erreur corrigé ec = e + (1/![]() m)
m) ![]() edt
edt
Il assure une action proportionnelle et intégrale " P.I " sur le système asservi.
Exemple de réalisation :
3.3. Augmentation de la précision et du degré de stabilité
On conjugue les effet des deux paragraphes précédents en montant en cascade un correcteur " P.D " et un correcteur " P.I ". L'ensemble est un correcteur " P.I.D ".

3.4. Remarques technologiques
Les erreurs de la chaîne d'action peuvent être éliminées par un correcteur intégral. Mais les erreurs dues au mélangeur et à la chaîne de retour affectent la précision sur la sortie. Les défauts d'offset de l'ALI du mélangeur, les imprécisions du capteur et des éléments du retour sont à considérer pour évaluer la précision réelle du système asservi.