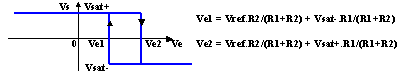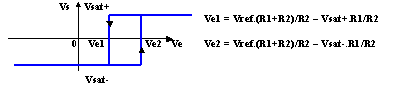1- Nature du fonctionnement 

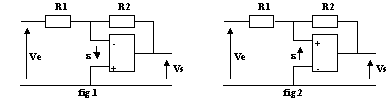
Étudions qualitativement la réponse à une perturbation qui fait croître depuis le point de repos où = 0. Au point de repos l'amplificateur linéaire intégré est en régime linéaire.

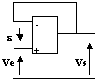
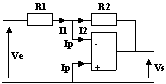
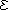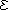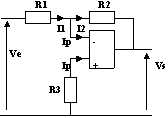
• fig.1 : Si augmente, l'ALI répond par une augmentation de Vs. Alors le circuit électrique par R2 et R1 fait décroître . Il y a donc une contre-réaction dans la structure, un fonctionnement en régime linéaire est possible.
• fig.2 : Si 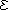augmente l'ALI répond par une augmentation de Vs. Alors le circuit électrique par R2 et R1 fait croître 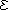. Il y a donc un emballement en saturation dans la structure, un fonctionnement en régime linéaire n'est pas possible.

 

 2- Structures fonctionnant en régime linéaire 
(Étude dans l'hypothèse de l'ALI parfait)

 2.1-Amplificateur inverseur 

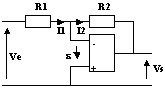
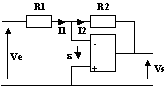
Du fait des hypothèses et du régime linéaire de l'ALI, I1 = I2 et = 0
Équations du circuit :
Ve = R1.I1
Vs = -R2.I1
Alors: Vs = - (R2/R1).Ve
La structure amplifie ou atténue le signal selon les valeurs des résistances et inverse la phase.
L'impédance d'entrée est R1. Il est donc difficile d'obtenir une très forte valeur.

 

 2.2-Amplificateur non inverseur 

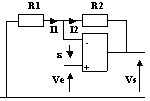
Du fait des hypothèses et du régime linéaire de l'ALI, I1 = I2 et = 0
Équations du circuit :
Ve = -R1.I1
Vs = -(R2+R1).I1
Alors: Vs = (1+R2/R1).Ve
La structure amplifie le signal sans inverser la phase.
L'impédance d'entrée est celle de l'ALI !
Avec R1 infinie et R2 = 0, on obtient le montage suiveur ci-dessous.

 

 2.3-Amplificateur suiveur 

Ici Vs = Ve, le montage est suiveur de tension.
L'impédance d'entrée est celle de l'ALI ! C'est l'intérêt de la structure.

 

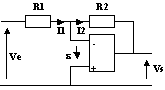
 2.4-Sommateur 

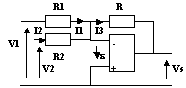
Du fait des hypothèses et du régime linéaire de l'ALI, I1+I2 = I3 et = 0
Équations du circuit :
V1 = R1.I1 et V2 = R2.I2
Vs = -R.I3. Alors Vs = -(R/R1).V1-(R/R2).V2
Si R1 = R2 = R : Vs = -(V1+V2)
La structure élabore la somme des signaux au signe près.

 

 2.5-Soustracteur 

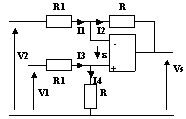
Du fait des hypothèses et du régime linéaire de l'ALI, I1 = I2, I3 = I4 et = 0
Équations du circuit :
V1.(R/R1+R) = V2.(R/R1+R) +VS.(R1/R1+R)
Donc : Vs = (R/R1).(V1 - V2)
La structure élabore une soustraction de signaux.

 

 2.6-Intégrateur 

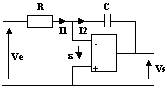
Du fait des hypothèses et du régime linéaire de l'ALI, I1 = I2 et = 0
Équations du circuit :
Ve = R1.i1
i1 = -C.dvs/dt
Donc : vs = -1/RC vedt
La structure élabore l'intégration du signal à un coefficient près.

 

 2.7-Dérivateur 

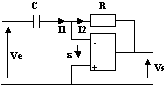
Du fait des hypothèses et du régime linéaire de l'ALI, I1 = I2 et = 0
Équations du circuit :
i1 = C.dve/dt
vs = -R.i1
Donc : vs = - RC.dve/dt
La structure élabore la dérivée du signal à un coefficient près.

 

 3- Structures fonctionnant en régime non linéaire 
(Étude dans le cas de l'ALI parfait)

 3.1-Comparateur 

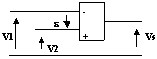
Si V1 > V2, < 0 et Vs = Vsat-
Si V1 < V2, > 0 et Vs = Vsat+

 

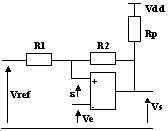
 3.2-Comparateur à hystérésis inverseur 

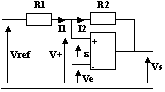
Du fait des hypothèses de l'ALI parfait, I1 = I2
V+ = Vref.R2/(R1+R2) + Vs.R1/(R1+R2)

Comme la structure ne peut pas fonctionner en régime linéaire :

Vs = Vsat+

• si 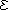> 0
• ou si V+ = Vref.R2/(R1+R2) + Vsat+.R1/(R1+R2) > Ve

Vs = Vsat-

• si 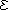< 0
• ou si V+ = Vref.R2/(R1+R2) + Vsat-.R1/(R1+R2) < Ve

Il y a donc deux valeurs particulières de Ve qui produisent le changement d'état de la sortie.

 3.3- Comparateur à hystérésis non inverseur 

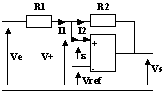
Du fait des hypothèses de l'ALI parfait, I1 = I2
V+ = Ve.R2/(R1+R2) + Vs.R1/(R1+R2)

Comme la structure ne peut pas fonctionner en régime linéaire :

Vs = Vsat+

• si 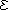> 0
• ou si V+ = Ve.R2/(R1+R2) + Vsat+.R1/(R1+R2) > Vref 
• ou encore si Ve > Vref.(R1+R2)/R2 - Vsat+.R1/R2

Vs = Vsat-

• si 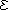< 0
• ou si V+ = Ve.R2/(R1+R2) + Vsat-.R1/(R1+R2)< Vref
• ou encore si Ve < Vref.(R1+R2)/R2 - Vsat-.R1/R2

Il y a donc deux valeurs particulières de Ve qui produisent le changement d'état de la sortie.

 

 4- Effet des imperfections de l'amplificateur intégré réel  

 4.1-Effet du décalage d'offset, exemple sur un amplificateur inverseur 

Dans l'hypothèse où le seul défaut de l'ALI est un décalage d'offset à l'entrée, en régime linéaire = ₀
En considérant Ve = 0 :
R1.I1 = ₀
Vs = -R2.I2 - ₀ = -R2.I1 - ₀
Donc Vs = -([R2/R1] +1). ₀ 
et en superposant le fonctionnement parfait : Vs = -(R2/R1).Ve -([R2/R1] +1). ₀
Par exemple si ₀ = 10mV et R2/R1 = 100, une composante continue de 1V s'ajoute au signal attendu !

 

 4.2-Effet des courants de polarisation sur un amplificateur inverseur 

Dans l'hypothèse où le seul défaut de l'ALI est un courant de polarisation sur les entrées, en régime linéaire = 0
En considérant Ve = 0 :
R1.I1 = 0 et I1 = 0
R2.I2 = -R2.Ip = -Vs
En superposant le fonctionnement parfait :
Vs = -(R2/R1) Ve +R2.Ip
Par exemple si R2 = 1M et Ip = 1µA, sur la tension de sortie s'ajoute une composante continue de 1V.

Pour éviter cet effet des courants de polarisation on peut placer une résistance R3 de compensation.

Dans l'hypothèse où le seul défaut de l'ALI est un courant de polarisation sur les entrées, en régime linéaire = 0
En considérant Ve = 0 :
R1.I1 = R3.Ip
R1.I1 +R2.(I1-Ip) = -Vs
Donc Vs = -R3.Ip -(R2.R3/R1)Ip +R2.Ip = 0 si R2 = R3.(1+R2/R1)
L'effet des courants de polarisation est compensé si R3 = R1.R2/(R1+R2) 

 

 4.3-Réponse en fréquence d'un amplificateur inverseur 

Dans l'hypothèse où le seul défaut de l'ALI est une amplification qui décroît aux fréquences élevées comme un premier ordre, en régime linéaire devient non négligeable et il faut en tenir compte.
Soit pour l'ALI Vs/= A/(1+jw/w₀)
Ve = R1.I1 -
Vs = -R2.I1 -
Vs = -(R2/R1).Ve - .([R2/R1]+1)
Vs[1 +(1+jw/w₀)(R2+R1)/R1.A] = -(R2/R1).Ve
Vs /Ve = -(R2/R1).(1/[1+{R1+R2}{1+jw/w₀}/R1.A])
Vs/Ve = -(R2/R1).(A.R1/[A.R1+R1+R2]).(1/[1+j{(R1+R2)/(A.R1+R1+R2)}w/w₀])
En considérant A.R1 grand devant R1 et R2 :
Vs/Ve = -(R2/R1).(1/[1+j{(R1+R2)/(A.R1)}w/w₀])

L'amplificateur inverseur se comporte en passe bas
de fréquence de coupure haute f₀.A.R1/(R1+R2)

Par exemple si A =10⁺⁵, R2=1000.R1 et f₀ = 100Hz (pour un TL081), la fréquence de coupure est de seulement 10kHz !

 

 4.4- Effet du slew rate sur un amplificateur inverseur 

    Soit un signal de sortie d'ALI tel que vs = 10 sin210⁺⁵t. La valeur maximale de dvs/dt est 2010⁺⁵ = 6,28Volts par µs. Pour que ce signal ne soit pas déformé il faut que l'ALI soit spécifié pour un slew rate supérieur au dvs/dt du signal à produire. Par exemple pour le TL081 dvs/dt = 13V/µs, valeur qui convient pour le signal vs.

 

 5- Les comparateurs rapides intégrés 
    Pour une structure comparateur le slew rate impose une transition très longue à chaque changement d'état. Par exemple alimenté sous +/-Vcc = 15V le TL081 qui est plutôt rapide exige près de 3µs pour chaque basculement !
    C'est la raison pour laquelle des composants intégrés nommés comparateurs ont été fabriqués. Les comparateurs intègrent des étages qui s'apparentent à ceux des circuits intégrés logiques, les temps de propagations sont donc beaucoup plus faibles. Mais ces circuits intégrés ne sont pas capables d'opérer en régime linéaire. Il ne peuvent être utilisés que pour les structures comparateur et comparateur à hystérésis.
    L'étage de sortie des comparateurs est en général de type collecteur ouvert. Une résistance de pull up externe est donc inévitable.

    Le transistor de l'étage de sortie est soit un transistor bipolaire NPN soit un transistor mosfet à canal N. L'émetteur ou la source du transistor est parfois accessible à l'utilisateur ou encore relié dans le circuit intégré à la masse ou à -Vcc. Ces indications sont essentielles à la compréhension du fonctionnement des structures.
    Dans les schémas de principe le symbole utilisé est le même que celui de l'ALI.

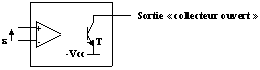
Exemple de structure interne :
Si > 0 le transistor est bloqué et équivalent à un interrupteur ouvert.
Si < 0 le transistor est conducteur et équivalent à un interrupteur fermé.
En sortie le courant ne peut être qu'entrant ou nul.
Quand le transistor est fermé le potentiel de son émetteur ou de sa source est appliqué en sortie.
Quand le transistor est ouvert le potentiel en sortie n'est pas imposé par le circuit comparateur, c'est le circuit électrique extérieur qui l'établit.
Exemple dans une structure comparateur à hystérésis inverseur :

Si le comparateur intégré est le LM311, son alimentation est symétrique +/-Vcc mais la sortie en collecteur ouvert utilise un transistor NPN dont l'émetteur est relié à la masse.
Dans ce cas la tension Vs = 0 si < 0 et Vs tend vers Vdd si > 0
Attention ! Le calcul des seuils de basculement doit considérer ces valeurs particulières de Vs.
On a intérêt à choisir Rp faible devant (R2 + R1), alors Vs ~ Vdd si > 0. Mais il faut tenir compte des courants dans le transistor de sortie du comparateur et ne pas prendre Rp trop faible. En général 470 < Rp < 10k
La configuration de cet exemple permet notamment une commande compatible avec des circuits logiques TTL ou CMOS. Il suffit de choisir pour Vdd la tension d'alimentation des circuits à attaquer.

 

Appliquette réalisée par JJ Rousseau

Exercices